PMTiles version 3: Hilbert Tile IDs and Run-Length Encoding
PMTiles is a single-file archive format for pyramids of tile data, like those used to power interactive maps. It’s designed to make storage and serving of planet-scale tiled maps simple using only affordable S3-like storage and HTTP Range Requests.
The physical world depicted in maps is infinitely detailed, but also not random like white noise. By exploiting redundancy in the physical world, we can make specialized formats for GIS more compact and efficient.
 Image: © 1977 EAMES OFFICE LLC
Image: © 1977 EAMES OFFICE LLC
The universe is sparse at all scales: dense clusters of unique features, with wide swaths of similarity
One step towards this in the first public version of PMTiles (specification version 2) was tile deduplication. The set of all OpenStreetMap PNG tiles will have many references to the same blue square representing the ocean.
Deploying PMTiles v2 for further real-world use cases and datasets has resulted in a few refinements to the design, the first of which is related to the internal tile addressing format for version 3. The new specification is being finalized and discussed on GitHub in time for the FOSS4G conference happening this year in Firenze, Italy.
Old vs. New Design
Refresher: the existing Entry record in PMTiles version 2 looks like this, inspired by the popular MBTiles SQLite-based format:
uint8 Z
uint24 X
uint24 Y
uint48 Offset
uint32 Length
Example: the entry Z=8 X=40 Y=87 points to byte range offset=4240340 length=32836 in a PMTiles file, which is a 32.7 kB PNG image near Vancouver, British Columbia:
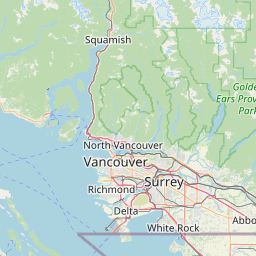
The v3 design simplifies the Entry struct to fewer and more standard column types:
uint64 TileId
uint32 RunLength
uint64 Offset
uint32 Length
The equivalent of the above in the new design would be TileId=36052 RunLength=1 Offset=4240340 Length=32836.
TileID
The TileId 36052 corresponds to the Z,X,Y position of 8,40,87. The calculation of ID uses a pyramid of Hilbert curves starting at TileId=0 for zoom level 0. The next zoom level, a 2x2 square, occupies the next four IDs in the ID space TileId=(1,2,3,4), the next level being the next 16 IDs, and so on.

In the example British Columbia tile above, the Z,X,Y position of 8,40,87 corresponds to the 14207th Hilbert curve position on level 8, which starts at TileID=21845.
The TileId is a convenient 64-bit integer that packs low zoom levels into the least significant bits. This makes it efficient to store in bitmap representations like Roaring, variable-length integer encodings, or constrained runtimes like JavaScript. The maximum representable tile zoom level in JavaScript numbers is 28.
RunLength
PMTiles v3 replaces Z,X,Y with the single TileID field, and also adds a new field RunLength.
The previous PMTiles design deduplicates repetitive tiles like blue ocean squares via multiple entries pointing to the same data. However, it can repeat the same entry millions of times for large regions of oceans, which cover 70% of the planet.
Ocean tiles are not only repetitive, but sparse and often contiguous in Hilbert space. This entry:
TileID=2578427,RunLength=107977,Offset=3650651795,Length=42
means that the 44 byte vector tile with a single square in the layer ocean is repeated over 100,000 times, starting at Z,X,Y=11,285,1311 and ending at 11,19,1304. This single contiguous sequence is represented by the yellow-green gradient in the planet image below:
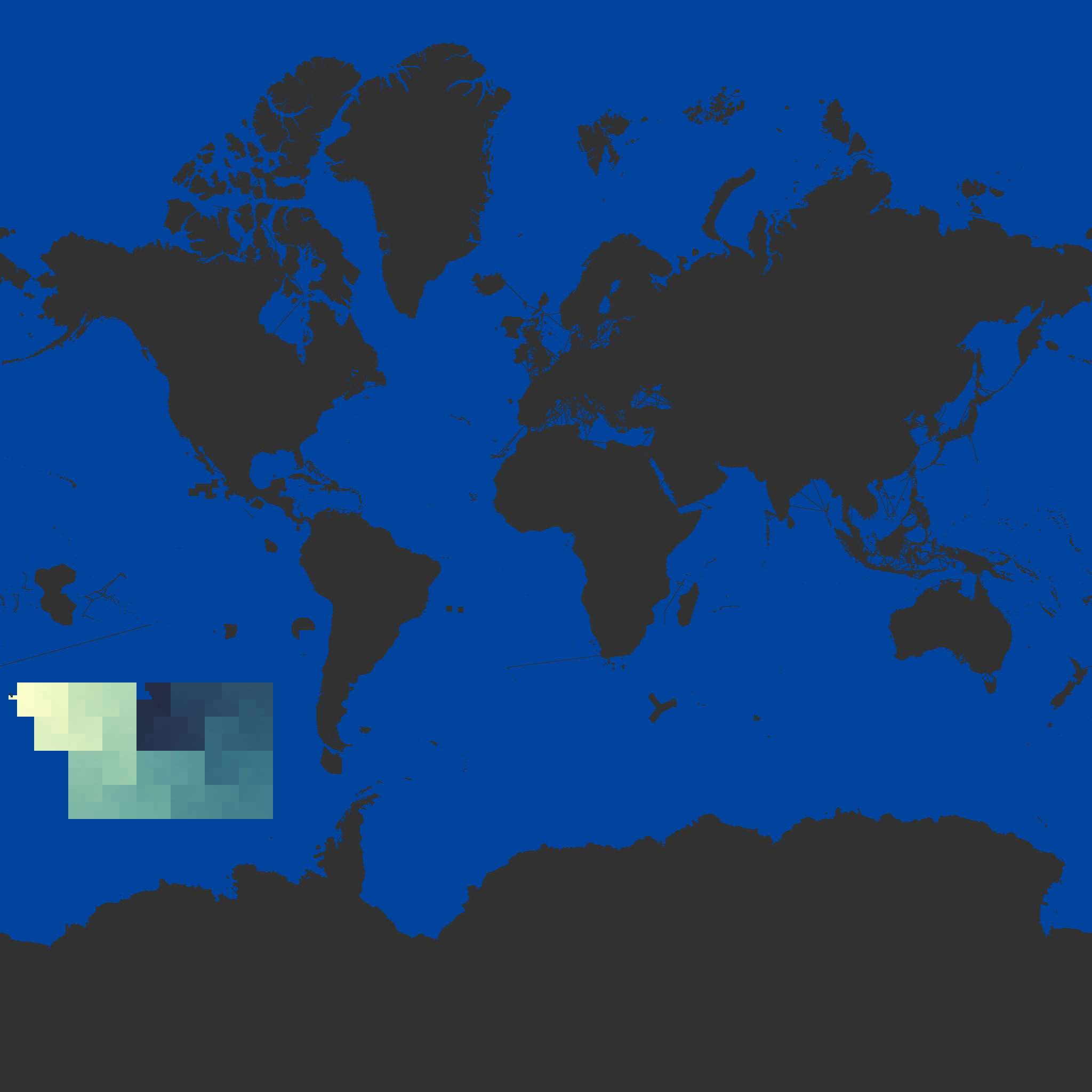
What previously required 107,977 separate directory entries, or 1.8 megabytes of storage, can now be repesented by a single 24 byte entry. This specific case of a 75,000x compression ratio is useful to minimize storage costs and transfer latency of map tiles, which can help developers build and deploy faster, more flexible maps.
The next post will address the design of compressed directories in PMTiles version 3.

Contiguous Hilbert runs